PERBANDINGAN TRIGONOMETRI
Trigonometri adalah ilmu matematika yang
mempelajari tentang sudut, sisi, dan perbandingan antara sudut terhadap
sisi. Dasarnya menggunakan bangun datar segitiga. Hal ini karena arti
dari kata trigonometri sendiri yang dalam bahasa Yunani yang berarti
ukuran-ukuran dalam sudut tiga atau segitiga.
Perbandingan Trigonometri Pada Segitiga
Sebuah segitiga dengan salah satu sudutnya berupa 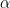 :
:

Sisi AB merupakan sisi miring segitiga
Sisi BC merupakan sisi depan sudut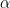
Sisi AC merupakan sisi samping sudut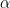
Sisi BC merupakan sisi depan sudut
Sisi AC merupakan sisi samping sudut
Di
sini kita akan mengenal istilah matematika baru, yaitu sinus (sin),
cosinus (cos), tangent (tan), cosecan (csc), secan (sec) dan cotangent
(cot), yang mana sinus merupakan kebalikan dari cosecan, cosinus
kebalikan dari secan dan tangent kebalikan dari cotangent.
Sinus,
Cosinus dan Tangent digunakan untuk menghitung sudut dengan
perbandingan trigonometri sisi di segitiga. Dengan gambar segitiga
diatas, nilai Sinus, Cosinus dan Tangent diperoleh dengan cara sebagai
berikut:
Sudut Istimewa
Berikut ini nilai sin, cos, dan tan untuk sudut istimewa:

Dalam Kuadran
Sudut dalam suatu lingkaran,
memiliki rentang 0° – 360°, sudut tersebut dibagi menjadi 4 kuadran,
dengan masing-masing kuadran memiliki rentang sebesar 90°.

- Kuadran 1 memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
- Kuadran 2 memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
- Kuadran 3 memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
- Kuadran 4 memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.
Perhatikan tabel trigonometri di bawah ini:

Identitas Trigonometri

Dalam suatu segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu  . Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
. Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
Bentuk ketiga yaitu  dibagi dengan
dibagi dengan 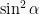 menjadi
menjadi 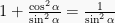 , dimana
, dimana  dan
dan  , sehingga diperoleh persamaan:
, sehingga diperoleh persamaan: 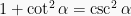 .
.
Contoh Soal Trigonometri
Tentukanlah nilai dari 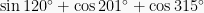 !
!
Jawab:
Jadi 








0 komentar:
Posting Komentar